My research often exploits computer simulations and numerical tools. We use fluid and kinetic plasma simulations to model turbulence, kinetic instabilities, magnetic reconnection, and the global evolution of plasma systems. Some of these numerical methods describe the plasma as a highly conducting fluid (magnetohydrodynamics), others treat the plasma as a collection of individual particles (particle-in-cell).
Our simulation work based on particle-in-cell simulations of turbulence has led to a number of press releases and articles:

• El Tiempo: Un colombiano lidera equipo que busca revelar secretos del plasma (in Spanish)
• Daily Mail online: Why solar winds are 10 TIMES hotter than expected when they hit Earth: Streams stay so hot because of magnetic connections that form in the turbulence, study reveals
• UKRI: Supercomputer simulations unlock an old space weather puzzle
• UCL: Supercomputer simulations unlock space weather puzzle

One of my current projects is the application of our computer code ALPS, which stands for Arbitrary Linear Plasma Solver. ALPS is a numerical solver for the full hot-plasma dispersion relation in a plasma with arbitrary background distribution functions. The numerical code determines the behaviour of kinetic plasma waves including relativistic effects. A particular strength of the code is that it can use velocity distribution functions measured by spacecraft and analyser their stability directly. More details can be found on http://alps.space. The ALPS code is publicly available at https://github.com/danielver02/ALPS, and the code paper can be found here.

Our solver NHDS (The New Hampshire Dispersion Relation Solver) calculates the linear hot-plasma dispersion relation in a plasma consisting of drifting bi-Maxwellians. The code is publicly available at https://github.com/danielver02/NHDS, and the code paper can be found here.
NHDS has been used in many studies to compare predictions from linear theory with spacecraft observations and simulations. One prominent example of this work has been featured in the following media articles:

• UCL: How magnetic waves interact with Earth’s bubble
• U Helsinki: New study models the transmission of foreshock waves towards Earth
• ISSI: Transmission of Foreshock Waves Through Earth’s Bow Shock

HolmMHD is a versatile numerical code that solves the nonlinear set of equations of isotropic, polytropic, ideal magnetohydrodynamics (MHD) on a Cartesian grid in three dimensions. It uses a hybrid spatial discretisation based on a fourth-order central scheme and the Rusanov scheme, which are mixed through a min-mod flux limiter.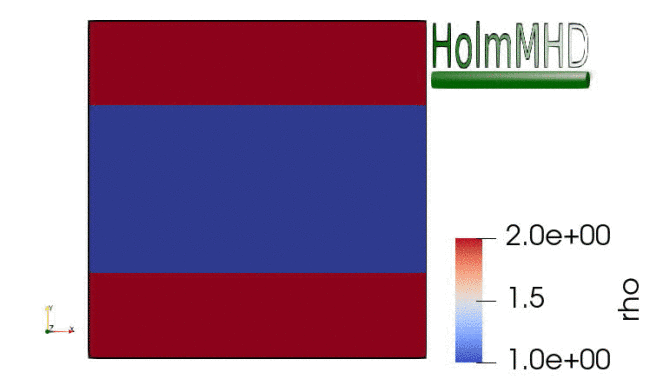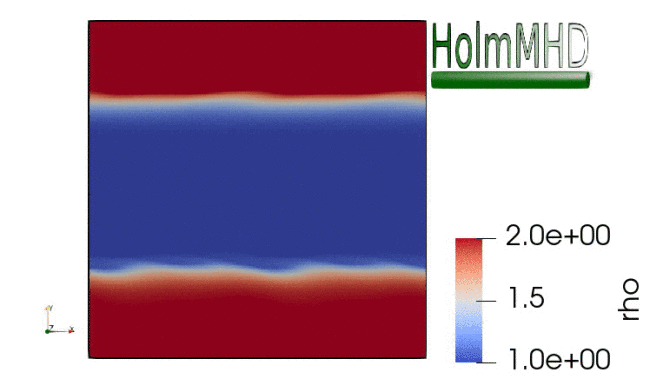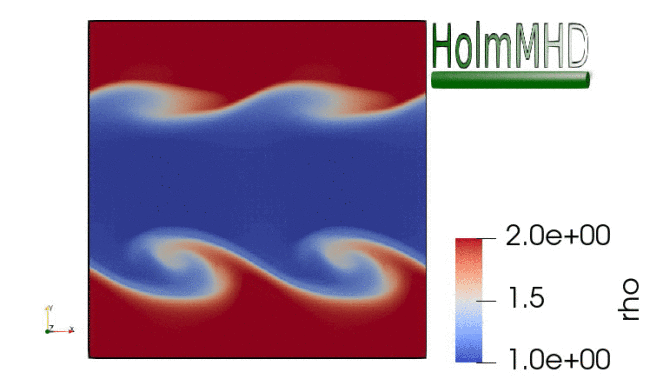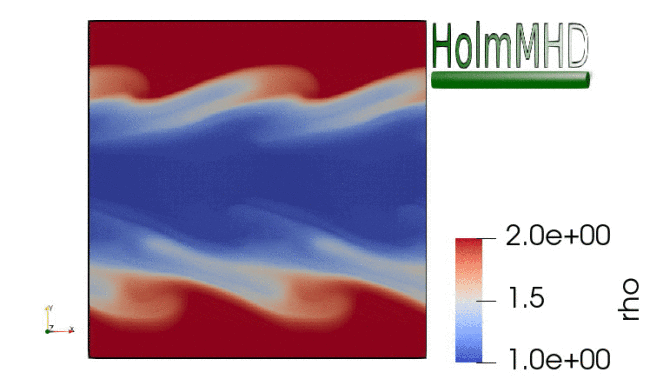
The code performs well on a range of benchmark problems such as a spherical hydro-blast wave, the Orszag-Tang vortex, Alfvén waves in one and three dimensions, the MHD aligned rotator, an isotropic three-dimensional decaying-turbulence setup, and the Kelvin-Helmholtz instability (shown on the right-hand side). The code is publicly available at https://github.com/danielver02/HolmMHD, and the code paper can be found here.